Nonparametric Regession

Nonparametric이므로, 가까운 $\vec{x}$는 가까운 $g(\vec{x})$값을 가질 것이라는 가정(Inductive Bias)을 제외하고는 어떠한 가정도 존재하지 않는다.
이 때의 $g(\vec{x})$ = $\vec{x}$의 neighbor들의 평균 label($r$).

Regressogram

---

Nonparametric Methods의 Histogram을 이용한 Regession model.

$$g(x)=\frac{\sum _{t}w(x,x^t)r^t}{\sum _{t}w(x,x^t)}$$

when: $w(x,x^t)=\{\begin{array}{ll}1& \text{if }{x}^t\text{ is in the same bin with }x\\ 0& \text{otherwise}\end{array}$

해당 $x$와 같은 bin에 있는 값들의 label의 평균으로 예측한다.

histogram을 활용한 모델이므로, Histogram과 동일한 단점을 가지게 된다.

Running Mean Smoother

---

Naive Estimator와 유사하다. (다른 Data point와의 거리) / (bin size)가 1보다 작을 경우에만 다른 Data point의 label 값을 평균하여 예측한다.

$$g(x)=\frac{\sum _{t}w(\frac{x-x^t}{b})r^t}{\sum _{t}w(\frac{x-x^t}{b})}$$

when: $w(u)=\{\begin{array}{ll}1& \text{if }|u|<1\\ 0& \text{otherwise}\end{array}$

bin size가 분모에 있으니, bin size가 커지게 된다면, 더 많이 포함시키게 된다.

Running Line Smoother

---

같은 bin안에 들어있는 Data point들을 이용해 각 bin 별로 Local Regression Line을 생성한다.

하지만, 여전히 불연속인 문제가 있고, Bin안의 값이 아예 없다면 정의가 되지 않는 문제가 발생한다.

Kernel을 이용하면, 멀리 있는 data point들은 영향을 덜 미치게 하여 weighted running line smoother($xK(x)$)를 만들 수는 있으나, 위의 문제가 동일하게 발생한다.

Kernel Smoother

---

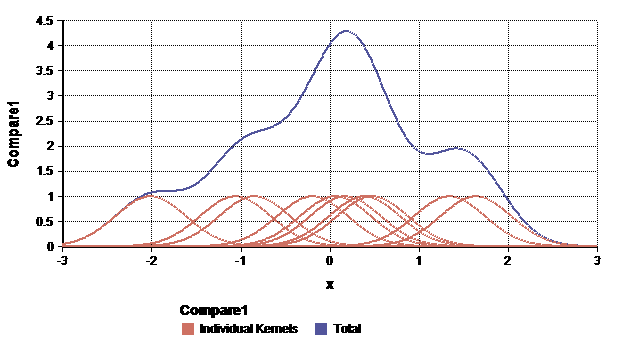
Kernel 함수를 이용한 Smoother.

$$g(x)=\frac{\sum _{t}K(\frac{x-x^t}{b})r^t}{\sum _{t}K(\frac{x-x^t}{b})}$$

만일 Guassian Kernel을 이용한다고 하면, 다른 점들($x^t$)의 Gaussian Distribution 더해 그 값을 이용한다.

• 모든 Sample을 이용하므로, 모든 Bin에서 정의된다.
• 연속으로 나타나게 된다.
• 하지만, 모든 점에 대해서 계산해야 하므로 계산량이 높아진다.

KNeighbor Smoother

---

k-nearest neighbor 기법을 이용한 smoother.

$$g(x)=\frac{\sum _{t}w(\frac{x-x^t}{d_k(x)})r^t}{\sum _{t}w(\frac{x-x^t}{d_k(x)})}$$

when: $w(u)=\{\begin{array}{ll}1& \text{if }|u|<1\\ 0& \text{otherwise}\end{array}$

• $k$번째 가까운 sample 까지의 거리(어찌보면 bin size라고 할 수 있다.)에 포함되는 갯수는 최소 1개 이상이므로 모든 bin에서 정의 된다.
• 또한, $k$개의 점까지에 대해서만 계산하므로 계산량이 줄어든다.

Oversmoothing and Undersmoothing

---

Overfitting과 Underfitting의 Nonparametric regression에서의 문제라고 볼 수 있다.

• Oversmoothing: $b\uparrow$ or $k\uparrow$: Bias가 낮아지지만 Variance가 낮아진다. (underfitting)
  • Smooth함이 올라감에 따라, 오히려 제대로 잘 표현하지 못하게 되는 것이다.
  • 즉, 데이터의 중요한 패턴을 과하게 smooth되므로 bias가 커지게 된다.
• Undersmoothing:$b\downarrow$ or $k\downarrow$: Bias가 낮아지지만 Variance가 높아진다. (overfitting)
  • 특정 샘플에 과하게 집중된 경우로, 만약 noise가 존재한다면 이까지 반영해 학습하게 될 수 있다.
  • 모델이 너무 복잡한 경우로, 작은 변화에도 민감해진다.

Regularized cost function

---

$$\sum _t(r^t-g(x^t){)}^2+\lambda {\int }_a^b{g^{\prime \prime }}^2(x)dx$$

: 기존의 MSE Error에, 곡률($g^{\prime \prime }$, 얼마나 빨리 변화하는지)을 더해 smooth함 또한 error에 포함시킨다.

• 곡률이 높아질 수록, 즉 변화율이 높을수록 smooth함이 떨어진다고 볼 수 있다.
• $\lambda$는 hyperparameter로, Validation 과정을 통해 찾을 수 있다.